EGit—Advanced topics

Rebase is another way of merging branches together. It does so without creating a merge commit and people like it because it gives a less complicated workflow (it doesn’t have all the merge commits).

It gets talked about a lot in Git polite society; generally because it is quite difficult to come to terms with.

I’m going to say right from the start that:

I don’t like REBASE—I recommend you don’t use it

Rebase is a little bit dangerous, it can leave unattached commit points floating around in the repository—just like resetting to an earlier commit and carrying on from there (I covered this is § 2.5.3). It can also change a commit and effectively create a replacement for it.

From an engineering point of view neither of these are good things, they spoil the traceability (someone could always use an unattached commit).

There are some rules for using the rebase. The first one is an absolute; you will read about it wherever rebase is discussed, it is this:

Rebase—the golden rule
Never use rebase with a branch that is available on a public repository.

If you want to merge two branches together using rebase and either branch is available in a remote repository (if, for example, it is stored on GitHub) then never use rebase.

Secondly, my rule:

Rebase—the Gledhill rule
Just don’t use rebase

Rebase is confusing; it changes what you think is a commit point to something else. Where remote repositories are concerned, this can get you into a lot of trouble with your colleagues—they will wonder where their commit point has gone and then they will shout at you.

All that said, this is how rebase works and how to use it:

To demonstrate the rebase, I will construct a simple repository with just one file in it.

Figure E.1   A simple workflow with two branches

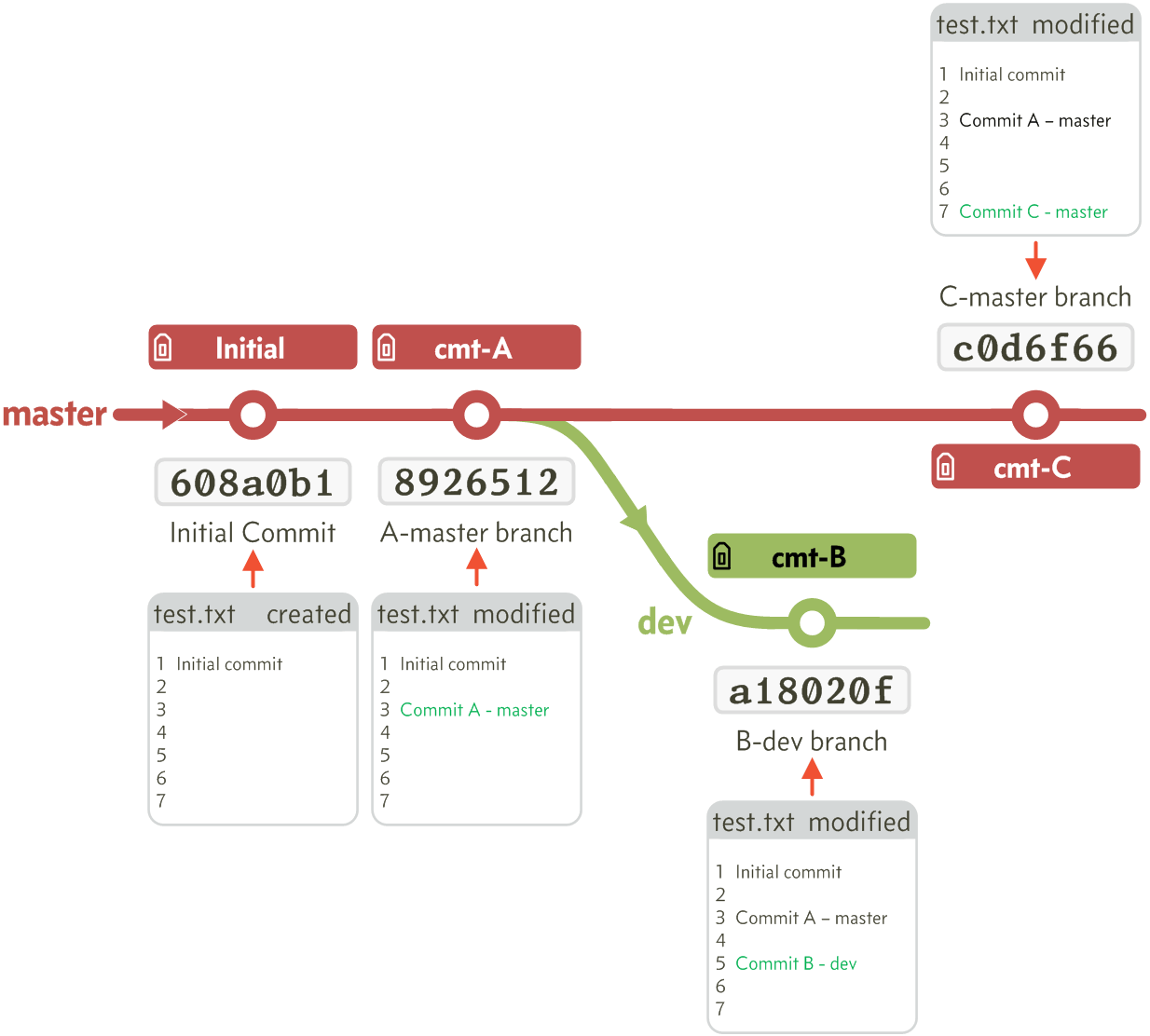
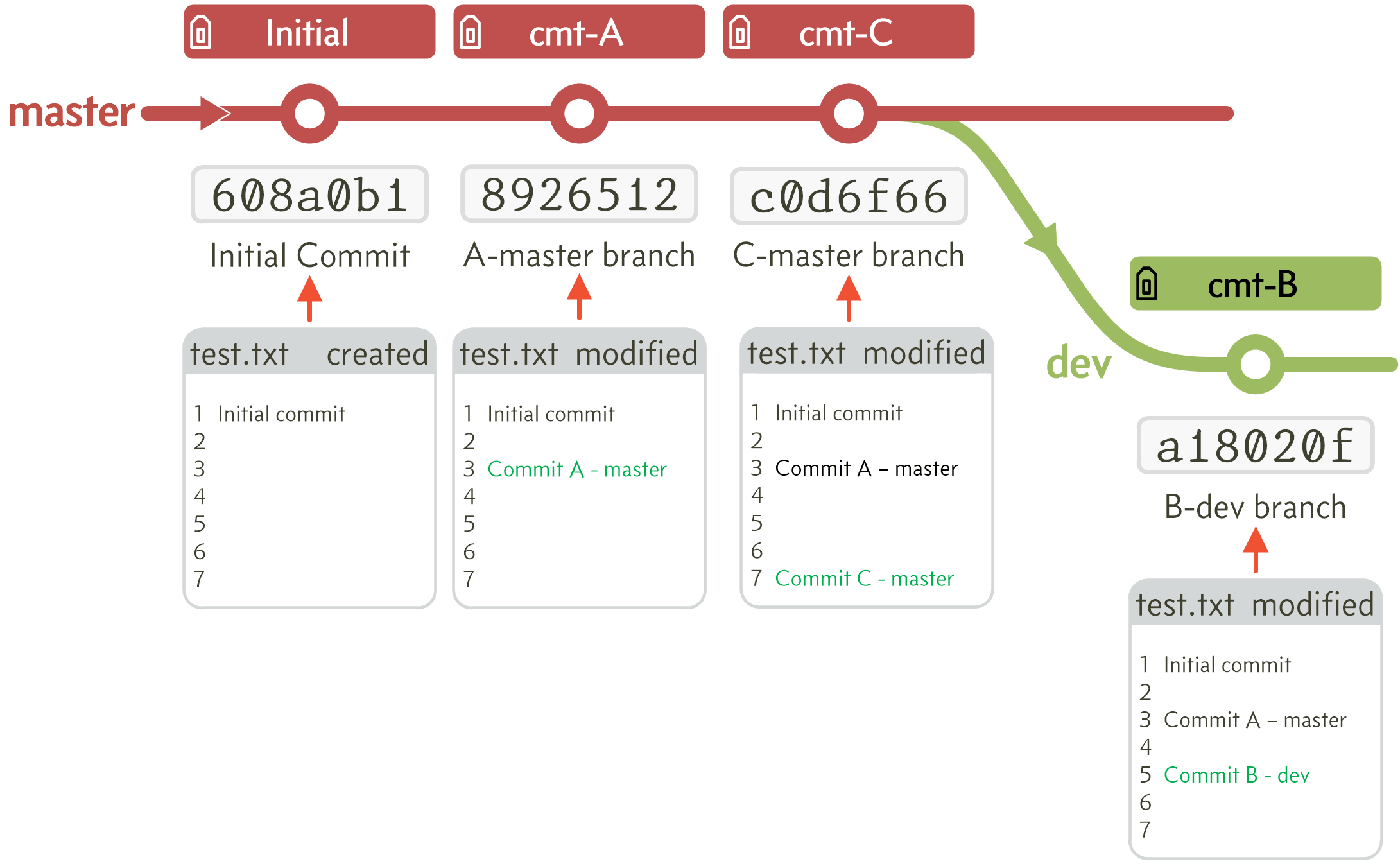
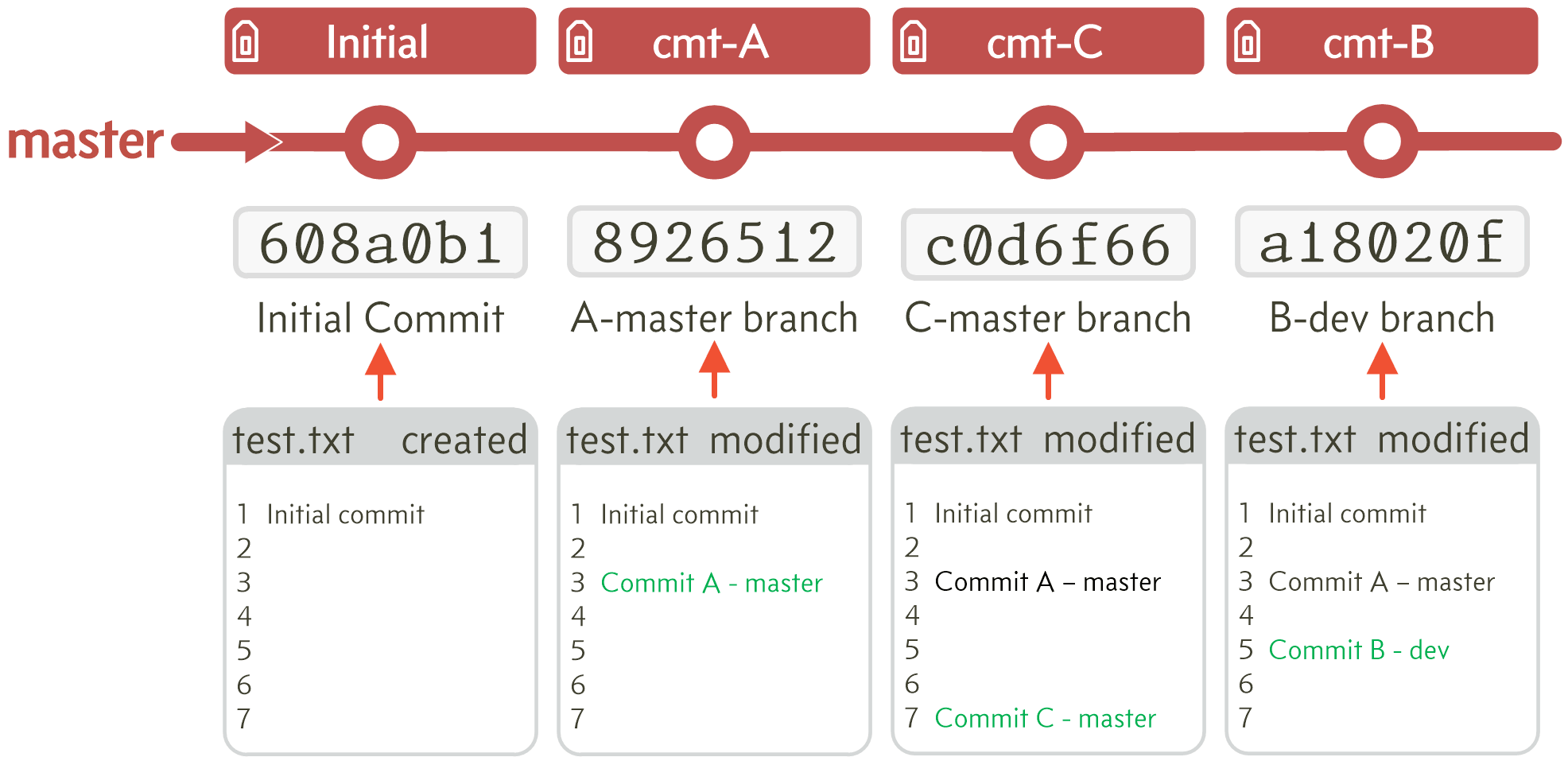
I created a file test.txt with seven lines, the first line being Initial commit. It was created on the master branch and committed with commit number [608a0b1].

The idea is that I will add extra text to the file at each commit and I will do this in two branches. I will then combine the branches using the rebase function.

After the initial commit, I make a second commit on the master branch. In this commit I modified line 3 of test.txt and added the text Commit A-master branch. This commit point has the number [8926512] and is tagged cmt-A.

Next I made a new dev branch from the master branch at the cmt-A commit point.

On the new dev branch I made a third commit, this time modifying line 5 to include the text Commit B-dev branch. This third commit point has the number [a18020f] and is tagged cmt-B.

Finally on the master branch I made a fourth commit, this time modifying line 7 to include the text Commit C-master branch. This fourth commit point has the number [c0d6f66] and is tagged cmt-C.

The full arrangement of commits and the contents of text.txt at each point can be seen in Figure E.1.

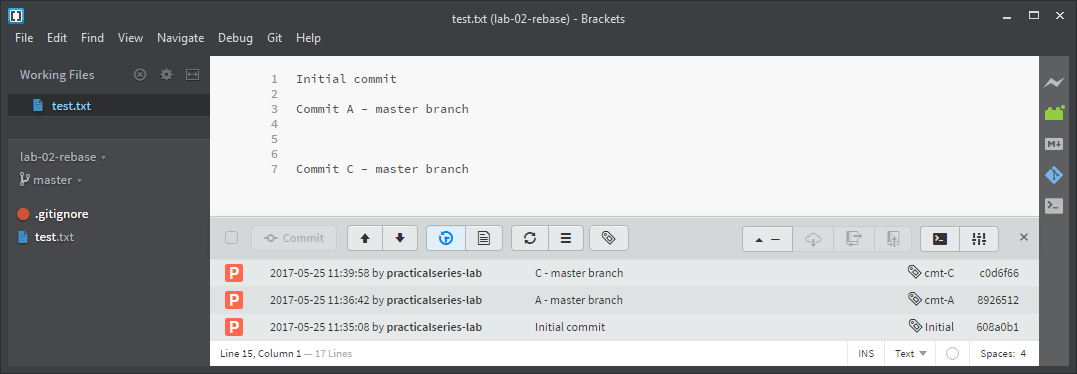
In Brackets the master branch looks like this:

Figure E.2   Master branch

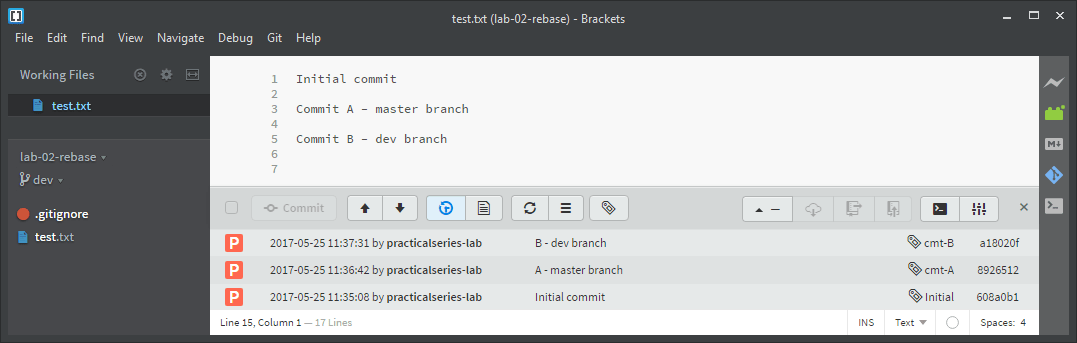
The dev branch looks like this:

Figure E.3   Dev branch

To summarise the master branch is missing commit B and the dev branch is missing commit C.

The next thing is the rebase itself. When we did a branch merge (back in section 6.7.1), we selected the master branch and merged the other branch into it.

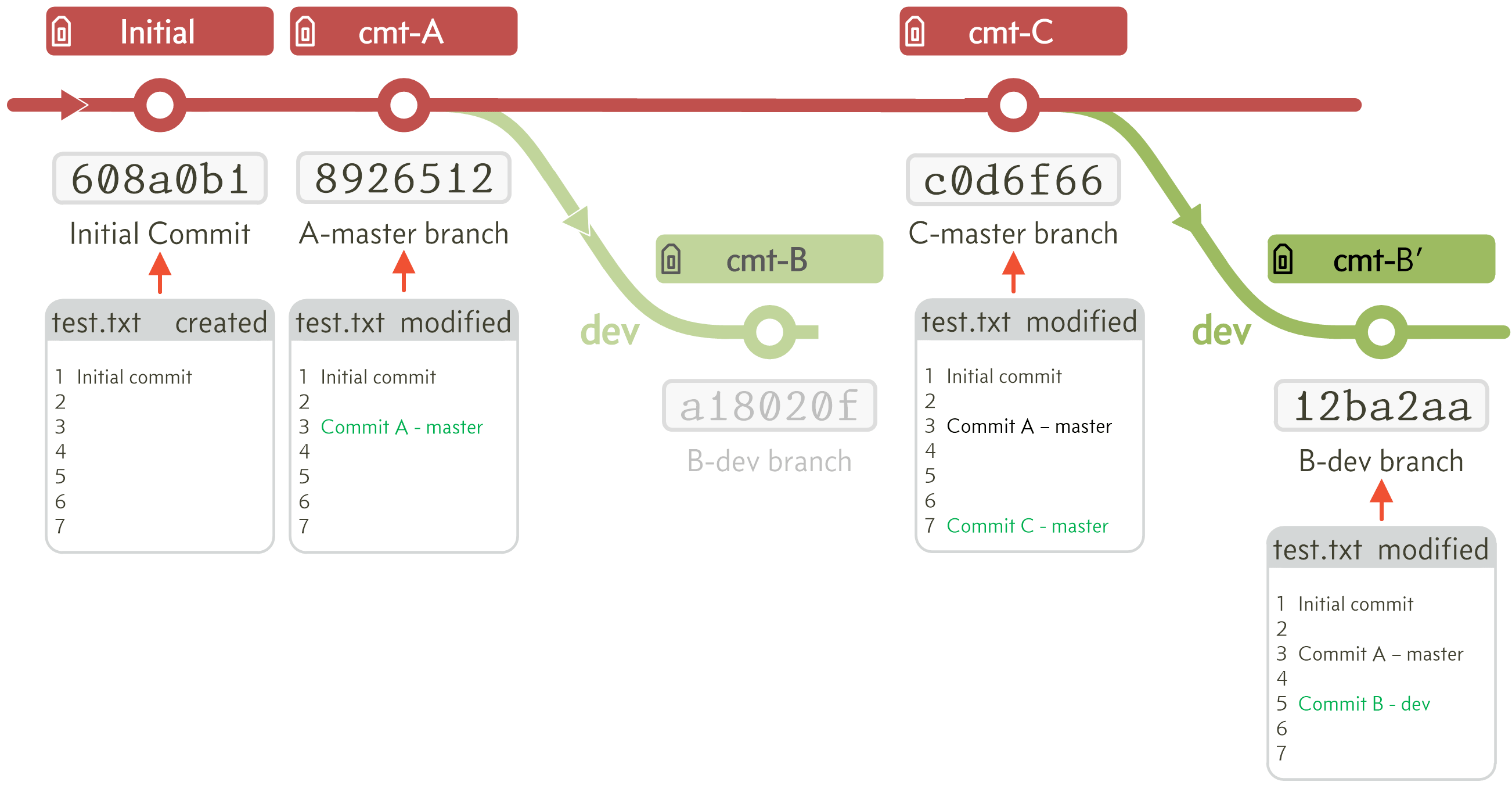
A rebase is the other way around; we start the rebase on the other branch (the dev branch in this case), the rebase effectively moves the point at which the rebasing branch deviated from the parent branch (master) to the end of the chain, it wants to do this:

Figure E.4   Theoretical workflow after a rebase

Essentially, the rebase unplugs the branch that is being rebased, and moves it to the tip of the other branch; in theory that is.

If we merged dev back into master at this point we would have:

Figure E.5   Theoretical workflow after a rebase and merge

The trouble is, that isn’t exactly what happens.

Here is the proper explanation:

The B commit was originally tied to the A commit (that’s where the branches originally diverged). It means that the moving the B commit to the end can’t be just a cut and paste. A rebase sequentially takes all the commits from the other branch and replicates (reapplies) them to the destination branch (dev in our case). This process has two main problems:

• By reapplying commits Git creates new ones. Those new commits, even if they bring in the same set of changes, will be treated as completely different commits and given new commit numbers.

• The rebase, when it reapplies commits, creates new ones, but does not destroy the old ones. It means that even after a rebase, the old commits will still be in the repository, and are still available.

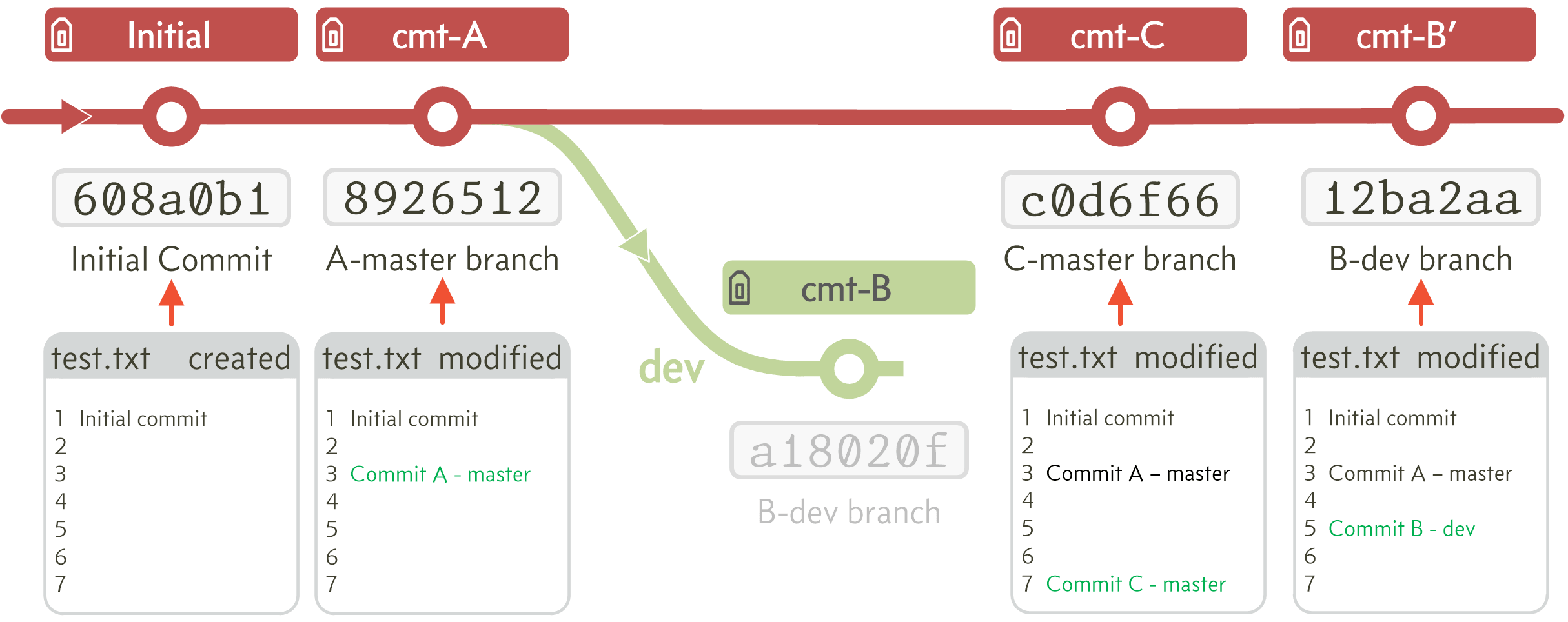
What actually happens is this:

Figure E.6   The actual workflow after a rebase

The dev branch has a completely new commit (I’ve called it cmt-B' that’s B prime); it even has a new commit number [12ba2aa].

The problem for me is that the previous commit (or commits if there was more than one on the dev branch) is not destroyed. It is still there, (it is not that easy to access, it would need a reset to find it), but someone could use it (particularly if they reset to a tag).

Once the rebase is complete, merging the dev branch with master gives (after a rebase, the merge will always work, it will be a fast-forward merge and needn’t create a merge commit):

Figure E.7   The actual workflow after a rebase and merge

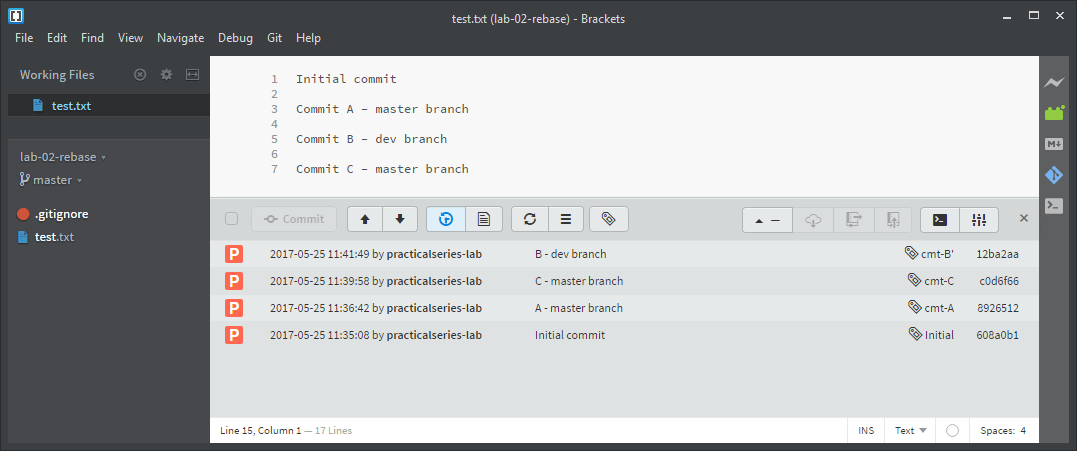
The final arrangement in Brackets (and the content of test.txt) is:

Figure E.8   The actual workflow after a rebase and merge in Brackets

I think it is confusing—think long and hard before using it.